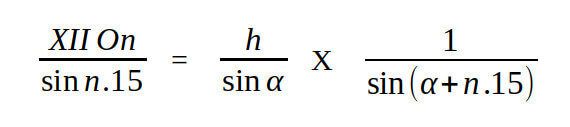Le cadran solaire « l’Unique » aux jardins de l’Europe
Une drôle de sculpture se situe à l’extrémité des Jardins de l’Europe, juste en face de l‘île aux cygnes et du lac d’Annecy. Il s’agit d’un gnomon polyorénome ou plus simplement d’un cadran solaire. Cet instrument permet de connaître l’heure qu’il est (la vraie heure, celle du soleil). C’est peut-être une futilité désormais, mais avoir l’heure juste et avoir la connaissance pour mesurer le temps était loin d’être partagé par les contemporains du Frère Arsène, le réalisateur de ce cadran complet.
Sommaire
Le gnomon en quelques mots
Le gnomon d’Annecy est inauguré le 22 juillet 1876. Le Frère Arsène, moine capucin né au début du 19ème siècle l’a imaginé 2 ans plus tôt. Le religieux décédera 3 ans après. Cet instrument de mesure réalisé en pierre est appelé « L’Unique » et se compose d’un socle, d’un piédestal et d’une étoile à 7 branches. L’ensemble est aligné et orienté, non pas par rapport au lac ou à d’autres éléments des Jardins de l’Europe mais pour être précisément placé par rapport à la latitude (25 minutes en avance avec l’heure de Greenwich).
Pour lire l’heure, il suffit de regarder l’ombre projetée par les pointes des branches de l’étoile. Encore faut-il savoir où regarder exactement car il y a des inscriptions, chiffres, schémas et traits sur les différentes faces du monument. Et forcément, il y a une explication qui se cache derrière chacun :
- sur la face supérieure (côté ciel), le cadran équinoxial indique l’heure en été ;
- sur la face inférieure, 2 cadrans indiquent l’heure en hiver. Un cadran permet d’avoir l’heure de 4h à 11h et l’autre de 13h à 20h ;
- le cadran au Sud donne l’heure de 6h à 18h tandis que le cadran « septentrionale » donne l’heure de 4 à 8h à l’Ouest et de 16h à 20h à l’Est ;
- Enfin, la courbe en forme de 8 allongé sur la face Sud permet de connaître les minutes à ajouter à l’heure.
Le gnomon d’Annecy est aussi capable d’indiquer lorsqu’il est midi dans quelques capitales européennes. Diverses inscriptions se déchiffrent facilement mais laissent perplexes la plupart des lecteurs : il s’agit de petites phrases sur la course du temps et un rappel que notre passage sur terre sera bien bref comparé à l’infini du temps.
Un gnomon se compose toujours d’au moins ‘une tige verticale qu’on appelle « style » qui projette l’ombre sur un élément situé plus bas (au sol, sur le socle). L’ombre peut être celle induite par le soleil mais aussi par la lune. Comme l’ombre change de longueur et de direction en fonction de la saison et du moment de la journée en fonction des déplacements des astres sur la voûte céleste, savoir interpréter l’ombre permet de connaître l’heure et la saison. Vous remarquerez qu’il n’y a plus de style sur le gnomon d’Annecy et que seules les pointes de l’étoile indiquent encore l’heure.
C’est le sculpteur Tavernier qui a réalisé l’instrument de mesure sur les indications du frère capucin. Plus tard, il a été restauré et certaines inscriptions ont été remplacées (les V se sont transformées en X – pour avoir des chiffres qui se suivent ?).
Amusez-vous donc à essayer de lire l’heure lorsque vous passerez à côté.
H.Bencker en a fait une description très complète en 1923. Le fichier est disponible ici. Dans son analyse, on voit encore les lettrages originaux. Son contenu, pas toujours très lisible, est reproduit ci-dessous.
Étude descriptive du GNOMON D’ANNECY
On remarque dans le Jardin public de la ville d’Annecy, comme monument élevé au bord du lac, une sorte de cadran solaire très curieux que son auteur, le P. Arsène, capucin d’Annecy, a intitulé : l’ « Unique ».
Nous nous proposons de le décrire succinctement dans ces quelques pages dont le but est d’initier les amateurs, aussi brièvement que possible, au fonctionnement de cette ingénieuse montre-solaire.
Dans un appareil aussi multiple que celui du frère Arsène on ne rencontre pas moins de 3 cadrans solaires.
Le 1er se trouve au centre de la face supérieure de l’étoile (voir Planche I) ; il sert en été, tant que le soleil demeure dans la partie septentrionale du ciel par rapport à l’Équateur, qui est aussi le plan de l’étoile. Il est dénommé « cadran équinoxial ». Les 2 autres sont disposés symétriquement l’un de l’autre sur la face inférieure de l’étoile à l’enracinement des branches élevées. (Voir Planche II.). Ils sont destinés à servir en hiver alors que le soleil demeure en dessous de l’Équateur (ou du plan de l’Étoile), plan dit « équinoxial inférieur ».
Une première famille de cadrans solaires comporte ceux pour lesquels le plan Q est perpendiculaire au style (A). (Pl. I.)
Une autre famille de cadrans comprend tous ceux pour lesquels le style et le plan Q sont parallèles (B).
Une autre famille englobe ceux pour lesquels le plan Q est incliné sur le style (C).
Les familles (B) et (C) se compliquent encore d’espèces symétriques ou obliques par rapport au méridien ou à l’horizontale.
Envisageons le cas où le plan de projection est à la fois parallèle au style et perpendiculaire au méridien (figure 1). Le plan OPO’P’ est le méridien de telle sorte que l’ombre O’P’ de OP coïncide avec le méridien NS. A une heure après-midi l’ombre de OP se fait en O¹P¹ car le soleil s’est déplacé, au-dessus de OP, vers l’Ouest de 15° à gauche du méridien ; aussi les angles O′O¹ et P′PP¹ sont-ils égaux à 15 degrés. À 2 heures après-midi, l’ombre de OP a lieu en O²P² de telle sorte que G′00² = P′OP² = 2×15° = 30° et ainsi de suite.
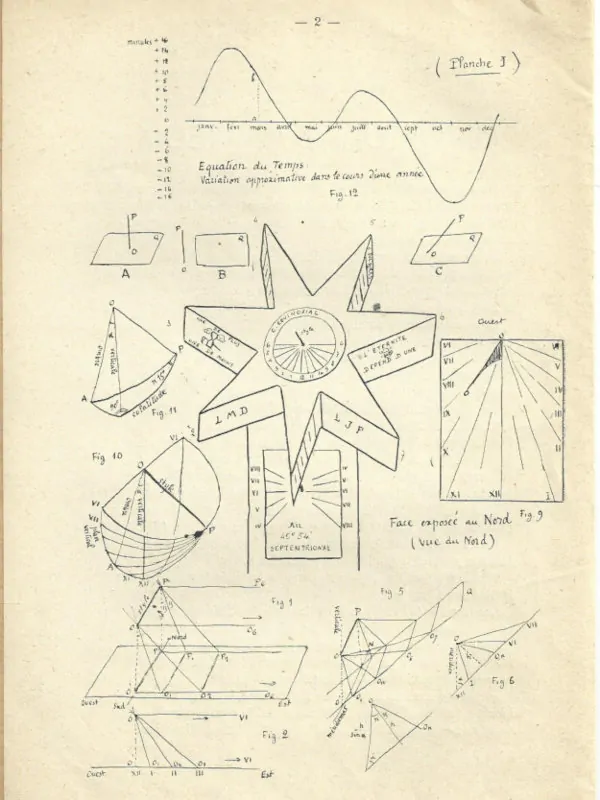
Planche I
Les distances successives qui séparent l’ombre portée de la méridienne peuvent se calculer, comme on le voit, sur la projection verticale de la figure 2 par la formule : O′O′n = h sin n × 15°
Formule dans laquelle h représente la distance du style OP au plan Q et n les nombres successifs entiers et fractionnaires.
Pour 6 heures du soir, l’ombre est rejetée à l’infini dans l’Est au-delà des limites matérielles du plan Q.
Nous verrons plus loin comment le Père Arsène a adapté un tel dispositif à son gnomon.
Dans le cas où le plan de projection est à la fois parallèle au style et parallèle au méridien, on obtient un gnomon analogue, seule la numération des traits de graduation change : la symétrie a lieu de part et d’autre de la VIᵉ heure et c’est la graduation correspondant à l’heure de midi qui échappe cette fois aux limites du cadran. L’écart des dimensions successives s’obtient toujours par la formule donnée précédemment.
Nous rencontrons deux applications de ce dispositif dans le gnomon du P. Arsène : ce sont les 2 cadrans gravés sur les 2 faces latérales du piédestal de l’Étoile. Le style est matérialisé par une arête OP (fig. 3 et 4) parallèle à la ligne des Pôles (et perpendiculaire au plan de l’Étoile) qui projette son ombre sur le plan méridien. Le côté « oriental » fonctionne de IV heures du matin à XI heures du matin. Le côté « occidental » fonctionne, en sens inverse, de I heure après-midi jusqu’à VIII heures du soir.
D’une manière générale, si le plan de projection Q, tout en restant parallèle au style, occupe une position quelconque oblique sur le méridien (fig. 5), on peut encore tracer les ombres horaires successives sur le plan Q en faisant la construction graphique qui est indiquée en coupe sur la figure 6.
Les distances des diverses divisions au point XII se calculent en appliquant l’analogie des sinus au triangle XII O On :
XII On = h sin n.15 coséc α coséc (α + n.15)
L’étoile du P. Arsène est une application générale et multiple de ce genre de projection : Les styles sont constitués par chacune des arêtes formant les pointes de l’Étoile. Le plan général de l’Étoile est parallèle à l’Équateur et chaque arête se trouve, par suite, parallèle à la ligne des pôles et susceptible de former gnomon avec les plans de projection qui sont constitués par chacune des facettes successives de l’Étoile dont les plans sont parallèles aux arêtes consécutives.
Pour voir comment les choses se passent, nous imaginerons qu’une étoile présentant une certaine épaisseur est centrée sur l’observateur O (fig. 6 bis). À un instant donné quelconque, le soleil S envoie sur chacune des arêtes des rayons lumineux, qui, à cause de son extrême distance, sont parallèles à une direction générale SO. Ces rayons lumineux déterminent sur les faces adjacentes de l’étoile des parties ombrées. Il suffira de graduer ces facettes en rapport avec les divisions horaires de notre cercle extérieur, qui vont de 15 en 15 degrés, pour obtenir les divisions correspondant aux heures vraies locales.
Le P. Arsène aurait pu choisir une étoile à 3 pointes ou à 5 pointes : il l’a choisie à 7 pointes pour plus de continuité dans les indications et aussi parce que le dispositif à 7 pointes possède des facettes qui sont de 6 en 6 dans le prolongement de l’autre de telle sorte que l’un de ces plans communs peut être disposé horizontalement (le plan 6-3 de la figure 7, par exemple). Par raison de symétrie, il a disposé la pointe inférieure(1) dans le méridien. Cela permet aussi d’utiliser un plus grand nombre de facettes graduées. Les pointes successives 1, 2, 3,… etc., sont distantes l’une de l’autre sur la circonférence de 3600/7= 51°26′ d’arc.
Les 2 branches supérieures 4 et 5 sont marquées « C. Polaires » (voir Planches II et III).
Les figures 7 et 8 indiquent par les lignes de construction tracées en pointillé, la façon de déterminer les graduations qu’il faut inscrire sur les facettes au moyen de directions tracées à partir de chacun des sommets et faisant entre elles des angles de 15 en 15 degrés à partir de l’horizontale (qui correspond à VI heures du matin ou du soir) ou de la verticale (qui correspond à XII, midi).
En traçant l’épure avec exactitude on pourrait discuter les valeurs des différents angles inscrits sur le cercle circonscrit à l’étoile heptacanthe, mais cette discussion n’offrirait ici aucun intérêt.
Les cadrans tracés par le P. Arsène sur les facettes de l’étoile portent aussi les indications des demi-heures par un trait un peu moins long que celui des heures. Les facettes non utilisées pour les graduations, ainsi que la face dorsale de l’étoile ont été remplies par des figures ou des inscriptions symboliques.
La planche II indique la majeure partie des graduations horaires, elle révèle bien l’aspect le plus général de l’appareil du P. Arsène.
Cette étoile étant disposée dans le plan de l’Équateur, les indications d’heures données par les ombres portées des arêtes se trouvent naturellement indépendantes de la distance qui sépare, dans son cercle horaire, le soleil de l’Équateur (Déclinaison) c’est-à-dire des saisons.
Le prisme qui porte l’étoile comporte encore un autre genre de cadran du type C dans lequel le plan de projection de l’ombre est oblique par rapport au style.
Celui de la face sud de ce prisme est un cadran solaire vertical et perpendiculaire au méridien (ce plan est appelé en astronométrie le « premier vertical »), de sorte que les traces d’ombre sur divers cercles horaires sont, sur lui, symétriques par rapport à la verticale méridienne XII. Le tracé de ces lignes d’ombre a été limité aux limites d’un rectangle (fig. 9).
Imaginons que l’on prenait sur la figure 10 des longueurs OP, O VI, O XII égales entre elles. Si, à partir de OP, on mène des cercles horaires successifs équidistants de 15 en 15 degrés on obtiendra sur le plan vertical les traces des ombres horaires en joignant le point O aux points VII, VIII,… XI.
Si par exemple le point A correspond à la 1ième heure à compter de midi, on pourra calculer l’écart angulaire α entre l’ombre OA et la verticale méridienne O XII en envisageant le triangle sphérique AP XII dans lequel l’angle en P est égal à n × 15°. Ce triangle sphérique est rectangle en XII (fig. 11) et le côté P XII est égal à la colatitude du lieu.
La formule des 4 éléments consécutifs de la trigonométrie sphérique appliquée à ce triangle donne la relation suivante : cotg α cos L = colg n. 15 + O
Cette formule nous permettra de tracer les angles α du cadran solaire en fonction de la latitude locale L.
L’appareil du P. Arsène a été tracé pour L = 45°54 de latitude septentrionale, ce qui correspond bien à la latitude d’Annecy (clocher de Saint-Maurice).
Sur la face nord du prisme on trouve un cadran analogue au précédent : il s’étend toutefois de part et d’autre et symétriquement de la ligne Est-Ouest, tandis que la verticale-méridienne n’y figure pas (Pl. 1).
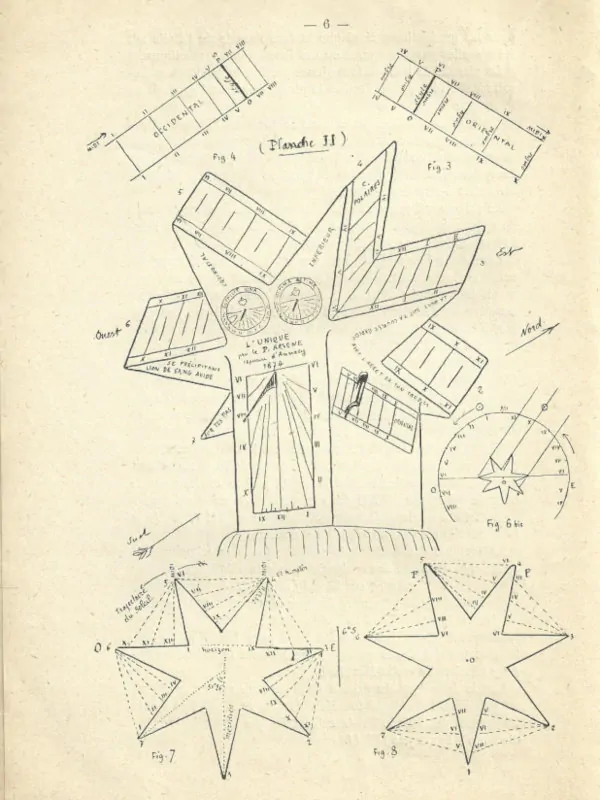
Planche II
Il est gradué de IV à VIII heures du matin à son côté Ouest alors que l’ombre est descendante.
Au côté Est, il est gradué de IV à VII heures du soir pour l’ombre montante.
Tel est l’« Unique » du P. Arsène, capucin d’Annecy ; qui constitue ainsi qu’on peut en juger par cette description un gnomon plutôt multiple ou montre-solaire polyrènome.
Nous limitons notre énumération des cadrans solaires aux applications qu’a utilisées le P. Arsène. Mais on conçoit que l’on puisse développer à l’infini les différents genres de projection mentionnés ci-dessus lorsqu’on utilise pour le tracé des plans qui sont obliques sur le méridien ou sur le premier vertical ; ou bien, lorsque au lieu d’utiliser un style OP qui soit parallèle à l’axe polaire, on choisit une tige verticale ainsi que cela était d’usage dans les formes primitives du gnomon.
Dans ce dernier cas, on obtient le cadran solaire dit « azimutal » dont le calcul, bien connu des navigateurs, a donné lieu à des tables qui varient avec la saison et avec la latitude.
Pour terminer, nous dirons quelques mots de la courbe fermée en forme de 8 qui se trouve tracée sur le socle (voir Planche IV) sur la face qui est exposée au sud. On désigne cette courbe sous le nom de « méridienne de temps moyen ».
On sait que nos horloges sont réglées, non pas sur le jour solaire vrai, mais sur le jour solaire moyen et que, par suite, elles indiquent le « temps moyen » ou « l’heure moyenne » et non pas le « temps vrai » ou « heure vraie » que donnent les cadrans solaires.
La différence entre le temps vrai et le temps moyen ou entre l’heure vraie et l’heure moyenne d’un même instant s’appelle l’« équation du temps ». Cette quantité varie selon la saison de 16 minutes à +14 minutes, de sorte que l’heure vraie ne s’écarte jamais de l’heure moyenne de plus de 16 minutes c’est-à-dire d’1/4 d’heure environ au maximum.
La courbe (fig. 12, pl. I) indique la variation approximative de l’équation du temps dans le cours d’une année.
Cette courbe donne, pour une date donnée, la correction qu’il y a lieu d’ajouter à l’heure vraie pour avoir l’heure moyenne. C’est-à-dire la quantité qu’il faut ajouter à l’indication donnée par le gnomon du P. Arsène pour obtenir l’heure moyenne d’Annecy.
Par exemple, le 15 mars il faudrait ajouter à l’indication du cadran la quantité ab = + 9 minutes.
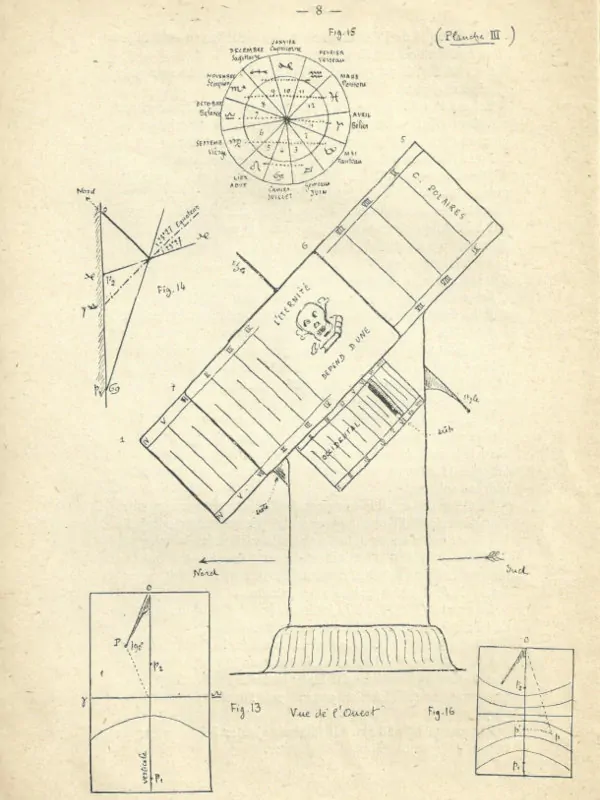
Planche III
La « méridienne de temps moyen », tracée sur le cadran lui-même, fait connaître automatiquement cette correction sans qu’il soit utile de recourir au graphique ci-dessus, ni à une table éphéméride.
Reprenons sur la fig. 13 le dispositif de la planche IV et étudions, en un jour donné, la trajectoire de l’extrémité p de l’ombre de OP.
Le jour de l’équinoxe, le rayon lumineux issu du soleil SP est parallèle à l’équateur et perpendiculaire à OP, et la trajectoire du point p est, ce jour-là, la ligne droite )|( perpendiculaire à la verticale figurée sur la figure 13.
En un jour quelconque, la direction du rayon lumineux SP fait un angle constant avec OP et engendre par conséquent un cône de révolution autour de OP et de sommet P. La section plane est donc une conique : généralement une arc d’hyperbole.
Aux solstices d’Été et d’Hiver, au moment où le soleil se trouve le plus écarté de l’Équateur (de 23°27′, angle qui correspond aux Tropiques du Cancer et du Capricorne) le point p’, ombre de P, passe aux points extrêmes de la verticale qu’il est susceptible d’atteindre et p¹ et p² (fig. 14).
La planche IV donne les arcs d’hyperbole parallèles aux trajectoires diurnes de l’ombre du style (extrémité) pour certaines saisons correspondant à des signes du zodiaque placés symétriquement comme cela est indiqué sur la figure 15.
Ces arcs d’hyperbole, par leur direction générale, permettent de connaître à la simple vue du cadran solaire en quel point, intermédiaire entre p¹ et p², sera coupée la verticale méridienne par la trajectoire de p. En effet, si à une heure quelconque l’ombre de P se fait en p, en estimant par la pensée l’arc pp’ parallèle à la direction générale des hyperboles intermédiaires, on trouvera le point p’ (fig. 16.).
La « méridienne de temps moyen » a été tracée en portant pour chaque jour soit à droite, soit à gauche de p’ selon le signe, la valeur de la correction ab de la figure 12 exprimée en minutes et à l’échelle adoptée pour le tracé du cadran solaire.
L’aspect général de la méridienne de temps moyen est donc une courbe fermée en forme de 8 s’étalant entre p¹ et p² et ne s’écartant jamais de plus de 16 minutes de la verticale à l’échelle du cadran solaire (pl. IV.).
Lorsque la trajectoire de l’extrémité de l’ombre du style coupe la méridienne de temps moyen il est midi moyen local, et cela fait aussi connaître la petite correction ab à apporter ce jour-là à l’heure vraie pour obtenir l’heure moyenne.
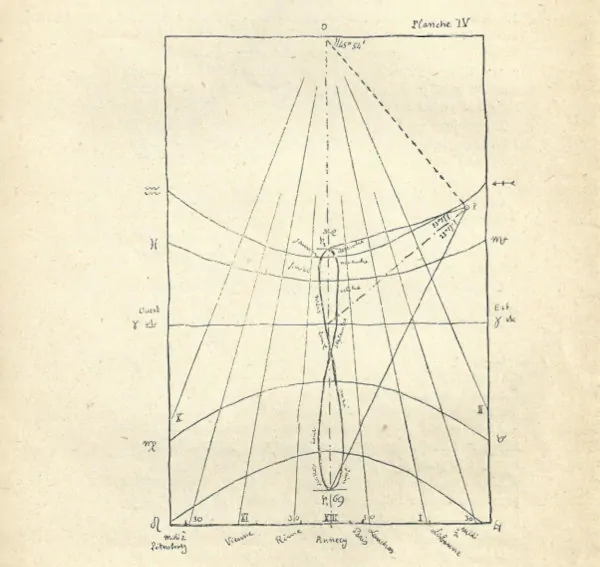
Planche IV
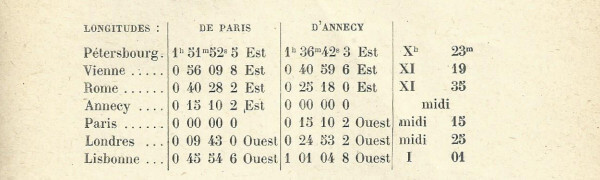
Le tableau de la plancge IV est enfin complété par l’indication de quelques traces d’ombres horaires provenant du style et destinées à marquer l’instant où il est midi vrai dans certaines capitales européennes. Ces éléments sont basés sur la différence parmanente de longitude entre la villle d’Annecy et ces diverses capitales qui s’exprime par un certain nombre d’heures à raison de une heure de temps par 15 degrés de différence de longitude.
Nous avons relevé les longitudes données ci-dessous dans les Positions Géographiques fournies par la Connaissance des Temps (année 1912).
La colonne hors tableau donne les heures du cadran correspondantes (heures vraies d’Annecy).
Pour terminer, nous savons que l’heure légale en France est non plus le temps moyen local, non plus que le temps moyen de Paris, mais le temps moyen de Greenwich (ou de Londres) qui retarde de 25 minutes sur le temps moyen d’Annecy.
La montre solaire du P. Arsène, telle qu’elle est établie, donne des indications qui sont toujours en avance de 25 minutes sur l’heure légale nonobstant la correction du temps vrai qui est fournie par le cadran auxiliaire de la face sud du piédestal.
La correction totale pour la mettre en concordance avec nos horloges varie dans le cours de l’année entre — 9 minutes et — 41 minutes, selon les saisons.
Paris, le 1er avril 1923.
H. BENCKER,
Lieutenant de vaisseau, au Service hydrographique de la Marine.